前提
前回の続き(趣味を作ろう(CTF-第四回) – 日曜エンジニアの学習記録)
CTF三面の問題を解く
①No23
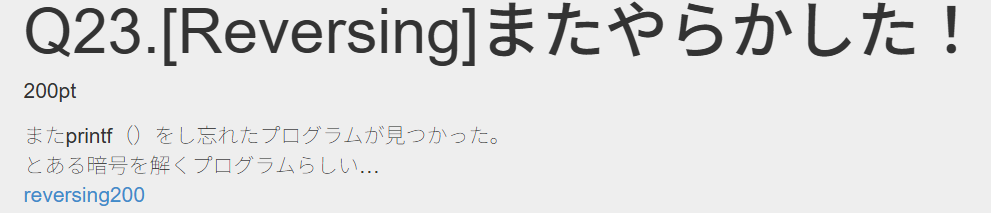
これは前回のやり方を”覚えていた”のでそのまま逆アセンブルで解いてしまいました‥
でも一応システマチックに解きたいと思っているので一旦fileコマンドで内容を確認してから解きました。
以下のコマンドを入力してフラグが出てきます。解決。
objdump -d -M intel --no-show-raw-insn --endian=little rev200 > test.log②No24

こういう問題の時の絶対~~しないでね系ってフリなのか分かんなくて困る
禁止している意図が分かれば判断できるんだけど初心者でそんな分別ないし‥
とりあえずこの手のやつはダメだったときに刑法の処罰対象なので迷ったらやらないという安全策で行く
私の悩みはともかく、以前解いた問題で表示されるwebページがあるのでそれをSQLインジェクションするのだと問題文からメタ読み
知っているSQLインジェクションが以下しか知らない(必ず真を返す文)のでパスワード欄に入力して即解決
' OR 1=1 --③No26

これを満たすxを求めればいいだけ?と思いつつ、見覚えのある式だったのでAIに聞いたら中国剰余定理という
大学の代数学の時間に出てきた定理だった。
確か上記を満たすxが一意に定まるという定理だったので、xは一つっていうことですね。
AIにこれを満たすコードをPythonに吐いてもらいました。以下が出ました。実行して解決。
a = 32134; b = 1584891; c = 193127; d = 3438478
x = a
while x % d != c:
x += b
print(x)④No29
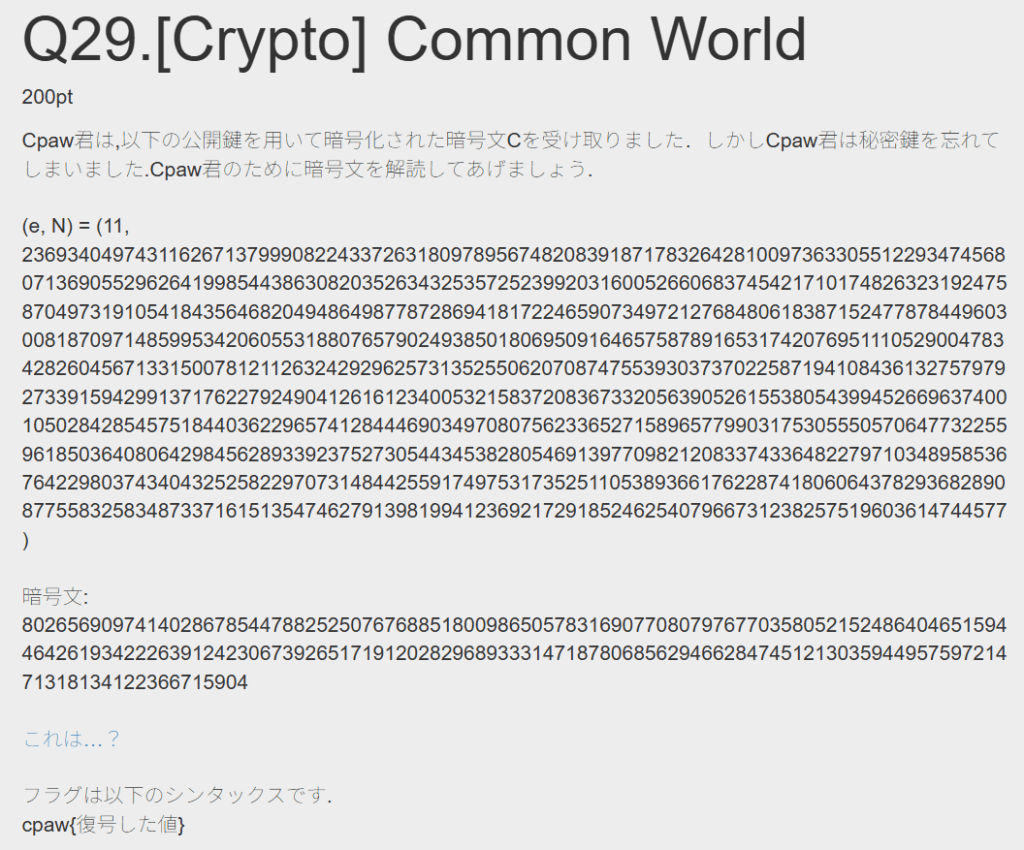
分からないのでとりあえず問題文のリンクを踏む

分かんない。とりあえず暗号文を復号すればよいことは分かるのでその方針で進める
とりあえず問題文が表しているものを理解したい。
e,Nが表していることが分からなかったのでAIに聞きました、分かりやすい。

そしてヒントの中で公開されている内容もNが問題文と同じだったのでその線で調べると、Common Modulus Attackという手法で
復号出来ることが分かった。
公開鍵暗号 RSA – Common Modulus Attack, 秘密鍵からの素因数分解 – ₍₍ (ง ˘ω˘ )ว ⁾⁾ < 暗号楽しいです
AIにN=11,N=13の情報を食わせて、Common Modulus Attackで復号できるプログラムを出力してとお願いしたら以下が出て解決
c1 = 80265690974140286785447882525076768851800986505783169077080797677035805215248640465159446426193422263912423067392651719120282968933314718780685629466284745121303594495759721471318134122366715904
c2 = 14451037575679461333658489727928902053807202350950440400755535465672646289383249206721118279217195146247129636809289035793102103248547070620691905918862697416910065303500798664102685376006097589955370023822867897020714767877873664
e1 = 11
e2 = 13
n = 236934049743116267137999082243372631809789567482083918717832642810097363305512293474568071369055296264199854438630820352634325357252399203160052660683745421710174826323192475870497319105418435646820494864987787286941817224659073497212768480618387152477878449603008187097148599534206055318807657902493850180695091646575878916531742076951110529004783428260456713315007812112632429296257313525506207087475539303737022587194108436132757979273391594299137176227924904126161234005321583720836733205639052615538054399452669637400105028428545751844036229657412844469034970807562336527158965779903175305550570647732255961850364080642984562893392375273054434538280546913977098212083374336482279710348958536764229803743404325258229707314844255917497531735251105389366176228741806064378293682890877558325834873371615135474627913981994123692172918524625407966731238257519603614744577
def egcd(a, b):
if a == 0:
return (b, 0, 1)
else:
g, y, x = egcd(b%a, a)
return (g, x - (b // a) * y, y)
def modinv(a, m):
g, x, y = egcd(a, m)
return x % m
def commom_world(c1, c2, e1, e2, n):
gcd, s1, s2 = egcd(e1, e2)
print gcd
print s1
print s2
if s1 < 0:
s1 = -s1
c1 = modinv(c1, n)
elif s2 < 0:
s2 = -s2
c2 = modinv(c2, n)
v = pow(c1, s1, n)
w = pow(c2, s2, n)
x = (v*w) % n
return x
print commom_world(c1, c2, e1, e2, n)進捗
三面クリア
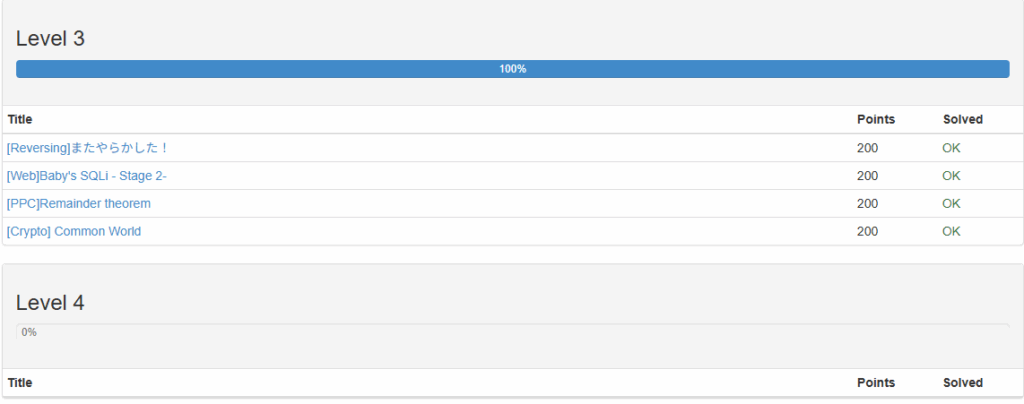
レベル4はまだ表示されないので開発中でしょうか?
俺たちの戦いは続く‥的な終わり方ですが、cpawに関しては終わりのようです。